-
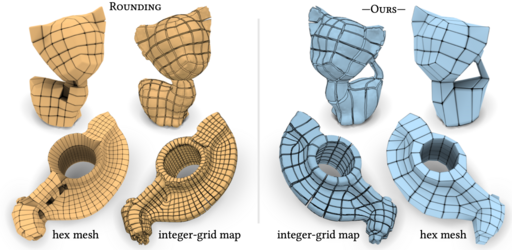
Quad Mesh Quantization Without a T-Mesh
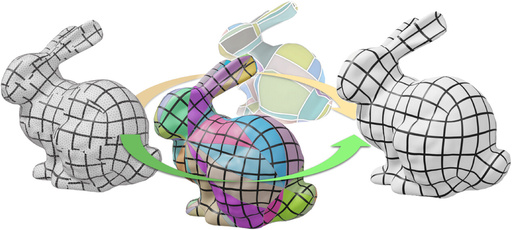
Grid preserving maps of triangulated surfaces were introduced for quad meshing because the 2D unit grid in such maps corresponds to a sub-division of the surface into quad-shaped charts. These maps can be obtained by solving a mixed integer optimization problem: Real variables define the geometry of the charts and integer variables define the combinatorial structure of the decomposition. To make this optimization problem tractable, a common strategy is to ignore integer constraints at first, then to enforce them in a so-called quantization step. Actual quantization algorithms exploit the geometric interpretation of integer variables to solve an equivalent problem: They consider that the final quad mesh is a sub-division of a T-mesh embedded in the surface, and optimize the number of sub-divisions for each edge of this T-mesh. We propose to operate on a decimated version of the original surface instead of the T-mesh. It is easier to implement and to adapt to constraints such as free boundaries, complex feature curves network etc.
@article{quantization-without-tmesh, author = {Coudert-Osmont, Yoann and Desobry, David and Heistermann, Martin and Bommes, David and Ray, Nicolas and Sokolov, Dmitry}, title = {Quad Mesh Quantization Without a T-Mesh}, journal = {Computer Graphics Forum}, doi = {https://doi.org/10.1111/cgf.14928}, } -
Expansion Cones: A Progressive Volumetric Mapping Framework
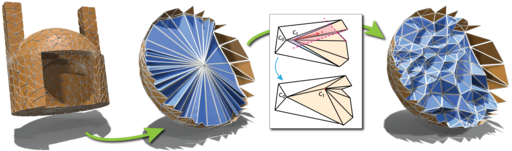
Volumetric mapping is a ubiquitous and difficult problem in Geometry Processing and has been the subject of research in numerous and various directions. While several methods show encouraging results, the field still lacks a general approach with guarantees regarding map bijectivity. Through this work, we aim at opening the door to a new family of methods by providing a novel framework based on the concept of progressive expansion. Starting from an initial map of a tetrahedral mesh whose image may contain degeneracies but no inversions, we incrementally adjust vertex images to expand degenerate elements. By restricting movement to so-called expansion cones, it is done in such a way that the number of degenerate elements decreases in a strictly monotonic manner, without ever introducing any inversion. Adaptive local refinement of the mesh is performed to facilitate this process. We describe a prototype algorithm in the realm of this framework for the computation of maps from ball-topology tetrahedral meshes to convex or star-shaped domains. This algorithm is evaluated and compared to state-of-the-art methods, demonstrating its benefits in terms of bijectivity. We also discuss the associated cost in terms of sometimes significant mesh refinement to obtain the necessary degrees of freedom required for establishing a valid mapping. Our conclusions include that while this algorithm is only of limited immediate practical utility due to efficiency concerns, the general framework has the potential to inspire a range of novel methods improving on the efficiency aspect.
@article{Nigolian:2023:SchrEx, author = {Nigolian, Valentin Z. and Campen, Marcel and Bommes, David}, title = {Expansion Cones: A Progressive Volumetric Mapping Framework}, journal = {ACM Transactions on Graphics}, volume = {42}, number = {4}, year = {2023}, publisher = {ACM}, address = {New York, NY, USA}, doi = {10.1145/3592421} } -
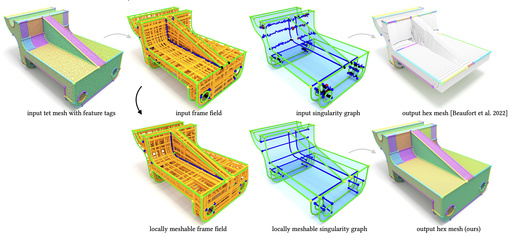
Locally Meshable Frame Fields
The main robustness issue of state-of-the-art frame field based hexahedral mesh generation algorithms originates from non-meshable topological configurations, which do not admit the construction of an integer-grid map but frequently occur in smooth frame fields. In this article, we investigate the topology of frame fields and derive conditions on their meshability, which are the basis for a novel algorithm to automatically turn a given non-meshable frame field into a similar but locally meshable one. Despite local meshability is only a necessary but not sufficient condition for the stronger requirement of meshability, our algorithm increases the 2% success rate of generating valid integer-grid maps with state-of-the-art methods to 58%, when compared on the challenging HexMe dataset [Beaufort et al. 2022]. The source code of our implementation and the data of our experiments are available at https://lib.algohex.eu.
@article{Liu:2023:locallymeshable, author = {Liu, Heng and Bommes, David}, title = {Locally Meshable Frame Fields}, journal = {ACM Transactions on Graphics}, volume = {42}, number = {4}, year = {2023}, publisher = {ACM}, address = {New York, NY, USA}, doi={10.1145/3592457} } -
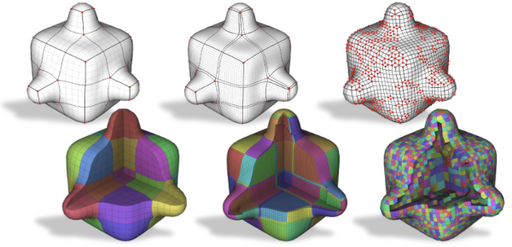
Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization
Subdividing non-conforming T-mesh layouts into conforming quadrangular meshes is a core component of state-of-the-art (re-)meshing methods. Typically, the required constrained assignment of integer lengths to T-Mesh edges is left to generic branch-and-cut solvers, greedy heuristics, or a combination of the two. This either does not scale well with input complexity or delivers suboptimal result quality. We introduce the Minimum-Deviation-Flow Problem in bi-directed networks (Bi-MDF) and demonstrate its use in modeling and efficiently solving a variety of T-Mesh quantization problems. We develop a fast approximate solver as well as an iterative refinement algorithm based on graph matching that solves Bi-MDF exactly. Compared to the state-of-the-art QuadWild implementation on the authors' 300 dataset, our exact solver finishes after only 0.49% (total 17.06s) of their runtime (3491s) and achieves 11% lower energy while an approximation is computed after 0.09% (3.19s) of their runtime at the cost of 24% increased energy. A novel half-arc-based T-Mesh quantization formulation extends the feasible solution space to include previously unattainable quad meshes. The Bi-MDF problem is more general than our application in layout quantization, potentially enabling similar speedups for other optimization problems that fit into the scheme, such as quad mesh refinement.
@article{Heistermann:2023:BiMDF, author = {Heistermann, Martin and Warnett, Jethro and Bommes, David}, title = {Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization}, journal = {ACM Transactions on Graphics}, volume = {42}, number = {4}, year = {2023}, publisher = {ACM}, address = {New York, NY, USA}, doi = {10.1145/3592437} } -
Hex-Mesh Generation and Processing: a Survey
In this article, we provide a detailed survey of techniques for hexahedral mesh generation. We cover the whole spectrum of alternative approaches to mesh generation, as well as post processing algorithms for connectivity editing and mesh optimization. For each technique, we highlight capabilities and limitations, also pointing out the associated unsolved challenges. Recent relaxed approaches, aiming to generate not pure-hex but hex-dominant meshes, are also discussed. The required background, pertaining to geometrical as well as combinatorial aspects, is introduced along the way.
@article{10.1145/3528223.3530123, author = {Br\"{u}ckler, Hendrik and Bommes, David and Campen, Marcel}, title = {Volume Parametrization Quantization for Hexahedral Meshing}, year = {2022}, issue_date = {July 2022}, publisher = {Association for Computing Machinery}, address = {New York, NY, USA}, volume = {41}, number = {4}, issn = {0730-0301}, url = {https://doi.org/10.1145/3528223.3530123}, doi = {10.1145/3528223.3530123}, abstract = {Developments in the field of parametrization-based quad mesh generation on surfaces have been impactful over the past decade. In this context, an important advance has been the replacement of error-prone rounding in the generation of integer-grid maps, by robust quantization methods. In parallel, parametrization-based hex mesh generation for volumes has been advanced. In this volumetric context, however, the state-of-the-art still relies on fragile rounding, not rarely producing defective meshes, especially when targeting a coarse mesh resolution. We present a method to robustly quantize volume parametrizations, i.e., to determine guaranteed valid choices of integers for 3D integer-grid maps. Inspired by the 2D case, we base our construction on a non-conforming cell decomposition of the volume, a 3D analogue of a T-mesh. In particular, we leverage the motorcycle complex, a recent generalization of the motorcycle graph, for this purpose. Integer values are expressed in a differential manner on the edges of this complex, enabling the efficient formulation of the conditions required to strictly prevent forcing the map into degeneration. Applying our method in the context of hexahedral meshing, we demonstrate that hexahedral meshes can be generated with significantly improved flexibility.}, journal = {ACM Trans. Graph.}, month = {jul}, articleno = {60}, numpages = {19}, keywords = {hexahedral mesh, base complex, block decomposition, multi-block, t-mesh, block-structured, volume mesh} } -
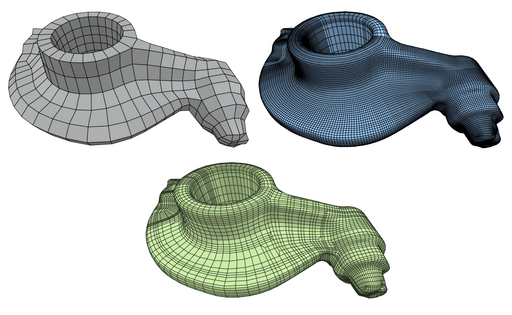
Volume Parametrization Quantization for Hexahedral Meshing
Developments in the field of parametrization-based quad mesh generation on surfaces have been impactful over the past decade. In this context, an important advance has been the replacement of error-prone rounding in the generation of integer-grid maps, by robust quantization methods. In parallel, parametrization-based hex mesh generation for volumes has been advanced. In this volumetric context, however, the state-of-the-art still relies on fragile rounding, not rarely producing defective meshes, especially when targeting a coarse mesh resolution. We present a method to robustly quantize volume parametrizations, i.e., to determine guaranteed valid choices of integers for 3D integer-grid maps. Inspired by the 2D case, we base our construction on a non-conforming cell decomposition of the volume, a 3D analogue of a T-mesh. In particular, we leverage the motorcycle complex, a recent generalization of the motorcycle graph, for this purpose. Integer values are expressed in a differential manner on the edges of this complex, enabling the efficient formulation of the conditions required to strictly prevent forcing the map into degeneration. Applying our method in the context of hexahedral meshing, we demonstrate that hexahedral meshes can be generated with significantly improved flexibility.
@article{10.1145/3528223.3530123, author = {Br\"{u}ckler, Hendrik and Bommes, David and Campen, Marcel}, title = {Volume Parametrization Quantization for Hexahedral Meshing}, year = {2022}, issue_date = {July 2022}, publisher = {Association for Computing Machinery}, address = {New York, NY, USA}, volume = {41}, number = {4}, issn = {0730-0301}, url = {https://doi.org/10.1145/3528223.3530123}, doi = {10.1145/3528223.3530123}, abstract = {Developments in the field of parametrization-based quad mesh generation on surfaces have been impactful over the past decade. In this context, an important advance has been the replacement of error-prone rounding in the generation of integer-grid maps, by robust quantization methods. In parallel, parametrization-based hex mesh generation for volumes has been advanced. In this volumetric context, however, the state-of-the-art still relies on fragile rounding, not rarely producing defective meshes, especially when targeting a coarse mesh resolution. We present a method to robustly quantize volume parametrizations, i.e., to determine guaranteed valid choices of integers for 3D integer-grid maps. Inspired by the 2D case, we base our construction on a non-conforming cell decomposition of the volume, a 3D analogue of a T-mesh. In particular, we leverage the motorcycle complex, a recent generalization of the motorcycle graph, for this purpose. Integer values are expressed in a differential manner on the edges of this complex, enabling the efficient formulation of the conditions required to strictly prevent forcing the map into degeneration. Applying our method in the context of hexahedral meshing, we demonstrate that hexahedral meshes can be generated with significantly improved flexibility.}, journal = {ACM Trans. Graph.}, month = {jul}, articleno = {60}, numpages = {19}, keywords = {hexahedral mesh, base complex, block decomposition, multi-block, t-mesh, block-structured, volume mesh} } -
Hex Me If You Can
HexMe consists of 189 tetrahedral meshes with tagged features and a workflow to generate them. The primary purpose of HexMe meshes is to enable consistent and practically meaningful evaluation of hexahedral meshing algorithms and related techniques, specifically regarding the correct meshing of specified feature points, curves, and surfaces. The tetrahedral meshes have been generated with Gmsh, starting from 63 computer-aided design (CAD) models from various databases. To highlight and label the diverse and challenging aspects of hexahedral mesh generation, the CAD models are classified into three categories: simple, nasty, and industrial. For each CAD model, we provide three kinds of tetrahedral meshes (uniform, curvature-adapted, and box-embedded). The mesh generation pipeline is defined with the help of Snakemake, a modern workflow management system, which allows us to specify a fully automated, extensible, and sustainable workflow. It is possible to download the whole dataset or select individual meshes by browsing the online catalog. The HexMe dataset is built with evolution in mind and prepared for future developments. A public GitHub repository hosts the HexMe workflow, where external contributions and future releases are possible and encouraged. We demonstrate the value of HexMe by exploring the robustness limitations of state-of-the-art frame-field-based hexahedral meshing algorithm. Only for 19 of 189 tagged tetrahedral inputs all feature entities are meshed correctly, while the average success rates are 70.9% / 48.5% / 34.6 % for feature points/curves/surfaces.
@article {10.1111:cgf.14608, journal = {Computer Graphics Forum}, title = {{Hex Me If You Can}}, author = {Beaufort, Pierre-Alexandre and Reberol, Maxence and Kalmykov, Denis and Liu, Heng and Ledoux, Franck and Bommes, David}, year = {2022}, publisher = {The Eurographics Association and John Wiley & Sons Ltd.}, ISSN = {1467-8659}, DOI = {10.1111/cgf.14608} } -
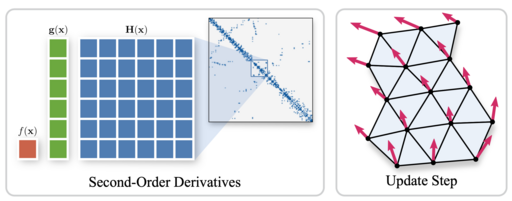
TinyAD: Automatic Differentiation in Geometry Processing Made Simple
Non-linear optimization is essential to many areas of geometry processing research. However, when experimenting with different problem formulations or when prototyping new algorithms, a major practical obstacle is the need to figure out derivatives of objective functions, especially when second-order derivatives are required. Deriving and manually implementing gradients and Hessians is both time-consuming and error-prone. Automatic differentiation techniques address this problem, but can introduce a diverse set of obstacles themselves, e.g. limiting the set of supported language features, imposing restrictions on a program’s control flow, incurring a significant run time overhead, or making it hard to exploit sparsity patterns common in geometry processing. We show that for many geometric problems, in particular on meshes, the simplest form of forward-mode automatic differentiation is not only the most flexible, but also actually the most efficient choice. We introduce TinyAD: a lightweight C++ library that automatically computes gradients and Hessians, in particular of sparse problems, by differentiating small (tiny) sub-problems. Its simplicity enables easy integration; no restrictions on, e.g., looping and branching are imposed. TinyAD provides the basic ingredients to quickly implement first and second order Newton-style solvers, allowing for flexible adjustment of both problem formulations and solver details. By showcasing compact implementations of methods from parametrization, deformation, and direction field design, we demonstrate how TinyAD lowers the barrier to exploring non-linear optimization techniques. This enables not only fast prototyping of new research ideas, but also improves replicability of existing algorithms in geometry processing. TinyAD is available to the community as an open source library.
@article{schmidt2022tinyad, title={{TinyAD}: Automatic Differentiation in Geometry Processing Made Simple}, author={Schmidt, Patrick and Born, Janis and Bommes, David and Campen, Marcel and Kobbelt, Leif}, year={2022}, journal={Computer Graphics Forum}, volume={41}, number={5}, } -
Cost Minimizing Local Anisotropic Quad Mesh Refinement
Quad meshes as a surface representation have many conceptual advantages over triangle meshes. Their edges can naturally be aligned to principal curvatures of the underlying surface and they have the flexibility to create strongly anisotropic cells without causing excessively small inner angles. While in recent years a lot of progress has been made towards generating high quality uniform quad meshes for arbitrary shapes, their adaptive and anisotropic refinement remains difficult since a single edge split might propagate across the entire surface in order to maintain consistency. In this paper we present a novel refinement technique which finds the optimal trade-off between number of resulting elements and inserted singularities according to a user prescribed weighting. Our algorithm takes as input a quad mesh with those edges tagged that are prescribed to be refined. It then formulates a binary optimization problem that minimizes the number of additional edges which need to be split in order to maintain consistency. Valence 3 and 5 singularities have to be introduced in the transition region between refined and unrefined regions of the mesh. The optimization hence computes the optimal trade-off and places singularities strategically in order to minimize the number of consistency splits — or avoids singularities where this causes only a small number of additional splits. When applying the refinement scheme iteratively, we extend our binary optimization formulation such that previous splits can be undone if this prevents degenerate cells with small inner angles that otherwise might occur in anisotropic regions or in the vicinity of singularities. We demonstrate on a number of challenging examples that the algorithm performs well in practice.
@article{Lyon:2020:Cost, title = {Cost Minimizing Local Anisotropic Quad Mesh Refinement}, author = {Lyon, Max and Bommes, David and Kobbelt, Leif}, journal = {Computer Graphics Forum}, volume = {39}, number = {5}, year = {2020}, doi = {10.1111/cgf.14076} } -
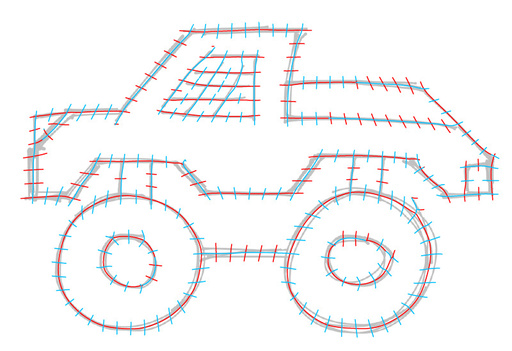
Integer-Grid Sketch Simplification and Vectorization
A major challenge in line drawing vectorization is segmenting the input bitmap into separate curves. This segmentation is especially problematic for rough sketches, where curves are depicted using multiple overdrawn strokes. Inspired by feature-aligned mesh quadrangulation methods in geometry processing, we propose to extract vector curve networks by parametrizing the image with local drawing-aligned integer grids. The regular structure of the grid facilitates the extraction of clean line junctions; due to the grid's discrete nature, nearby strokes are implicitly grouped together. We demonstrate that our method successfully vectorizes both clean and rough line drawings, whereas previous methods focused on only one of those drawing types.
@Article{SBBB20, author = "Stanko, Tibor and Bessmeltsev, Mikhail and Bommes, David and Bousseau, Adrien", title = "Integer-Grid Sketch Simplification and Vectorization", journal = "Computer Graphics Forum (Proceedings of the Eurographics Symposium on Geometry Processing)", number = "5", volume = "39", pages = "149--161", month = "jul", year = "2020", keywords = "line drawing, vectorization, grid parametrization" }