Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization

ACM Transactions on Graphics (SIGGRAPH 2023)
Martin Heistermann, Jethro Warnett, David Bommes

Materials

Note: The dataset is available both as .zip and as .tar.zst. The contents are identical, but the latter is smaller. To unpack, you can use tar xf file.tar.zst, but you need to have zstandard installed (available via homebrew and apt-get (as zstd)

SIGGRAPH Fast Forward video (20s)

Abstract

Subdividing non-conforming T-mesh layouts into conforming quadrangular meshes is a core component of state-of-the-art (re-)meshing methods. Typically, the required constrained assignment of integer lengths to T-Mesh edges is left to generic branch-and-cut solvers, greedy heuristics, or a combination of the two. This either does not scale well with input complexity or delivers suboptimal result quality. We introduce the Minimum-Deviation-Flow Problem in bi-directed networks (Bi-MDF) and demonstrate its use in modeling and efficiently solving a variety of T-Mesh quantization problems. We develop a fast approximate solver as well as an iterative refinement algorithm based on graph matching that solves Bi-MDF exactly. Compared to the state-of-the-art QuadWild implementation on the authors' 300 dataset, our exact solver finishes after only 0.49% (total 17.06s) of their runtime (3491s) and achieves 11% lower energy while an approximation is computed after 0.09% (3.19s) of their runtime at the cost of 24% increased energy. A novel half-arc-based T-Mesh quantization formulation extends the feasible solution space to include previously unattainable quad meshes. The Bi-MDF problem is more general than our application in layout quantization, potentially enabling similar speedups for other optimization problems that fit into the scheme, such as quad mesh refinement.

Selected figures

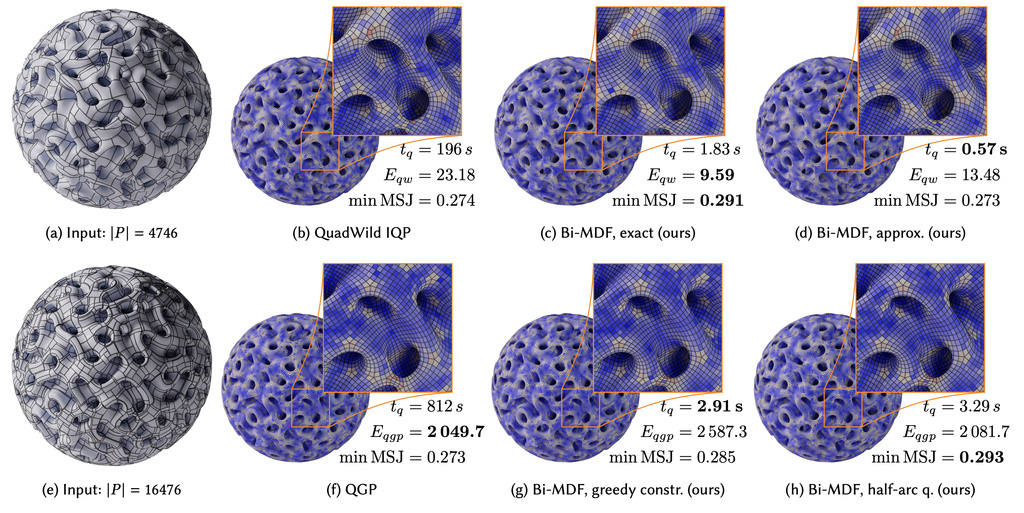
Fig 1. Bi-MDF optimization provides orders-of-magnitude faster performance when quantizing polygonal (a) and quadrangular (e) T-meshes of this genus-548 gyroid model. Colors indicate element quality as measured by the minimum scaled Jacobian (MSJ). For the QuadWild [Pietroni et al. 2021] based results (b-d) we chose 𝛼 = 0.005 and no singularity alignment. (b) uses QuadWild’s default settings for clustering (𝑛 = 300), per-cluster time limit (200 s), and early abort heuristics. With clustering and abort heuristics disabled, QuadWild achieves an energy 𝐸𝑞𝑤 = 9.70 with a duality gap of 23.8% after reaching a 24 h time limit. Figures (f-g) demonstrate performance compared to QGP [Campen et al. 2015]. Bi-MDF with greedily chosen separation constraints (g) is fastest but leads to slightly worse results. Half-arc quantization (h) expands the feasible region of allowed quantizations by quantizing either side of an arc separately.

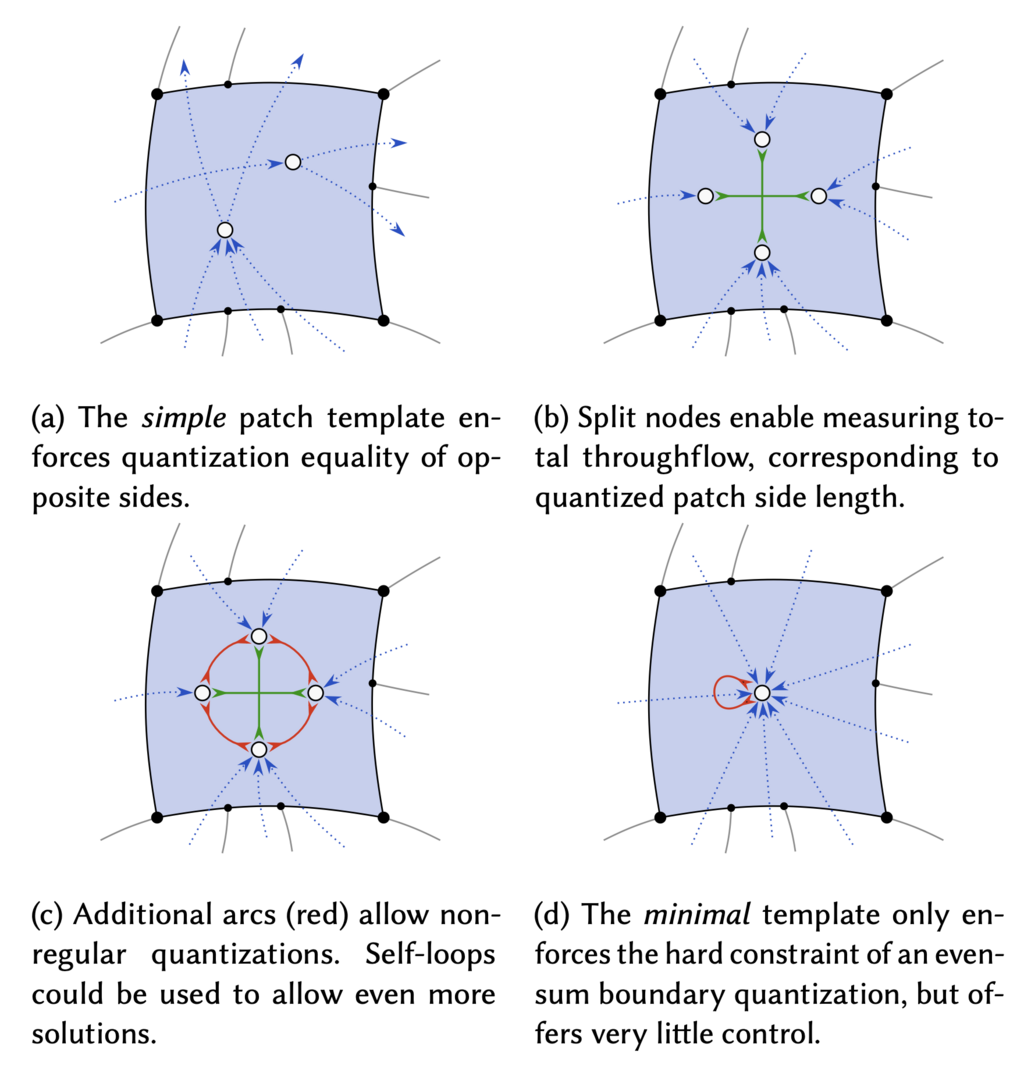
Fig. 10. A selection of bi-flow network templates for quadrangular patches. Starting with (b), edge orientations are chosen such that patches only receive inflow from their neighbors. This simplifies network assembly.

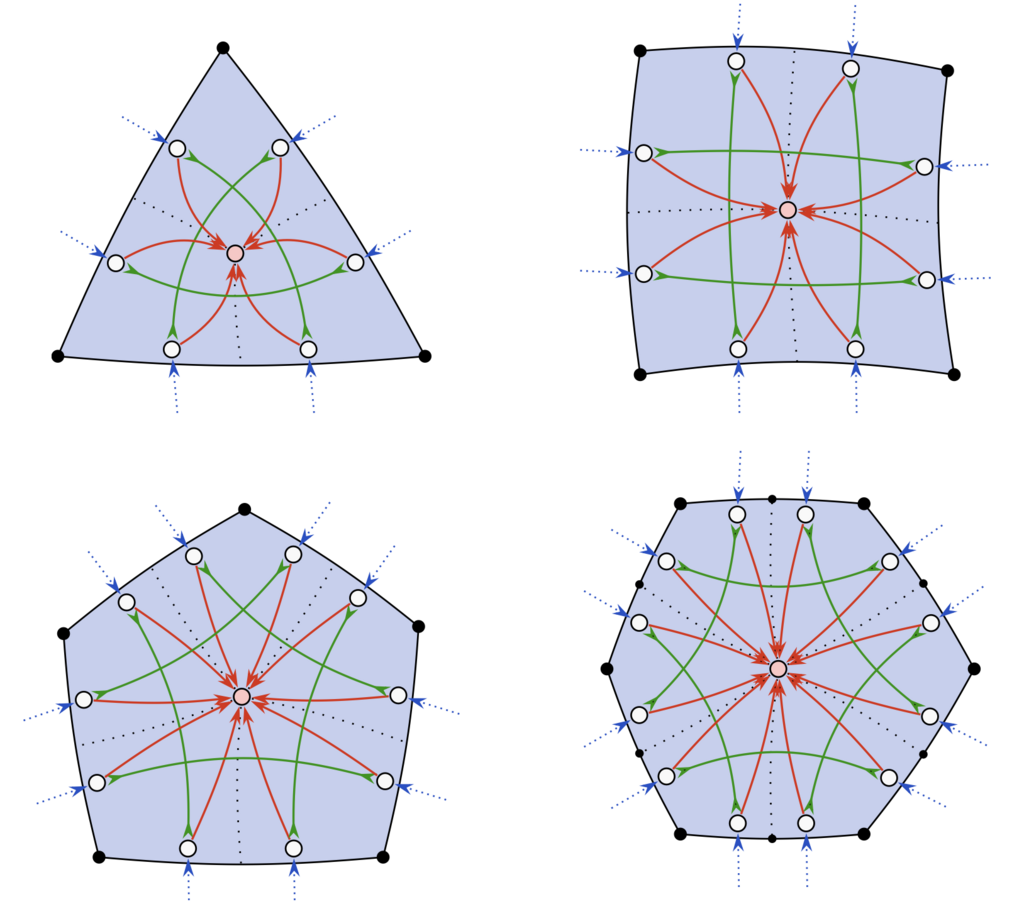
Fig. 13. Templates for polygonal patches of valence 3 to 6 with paired sides. Outer-edges (blue, dashed) connect to other patches or the boundary. An emergency node (pink) allows for non-regular quantizations by sinking even amounts of flow using a tail-tail self-loop (omitted here to reduce clutter) from emergency arcs (red) that have a target of zero, are unbounded, and carry a high weight.

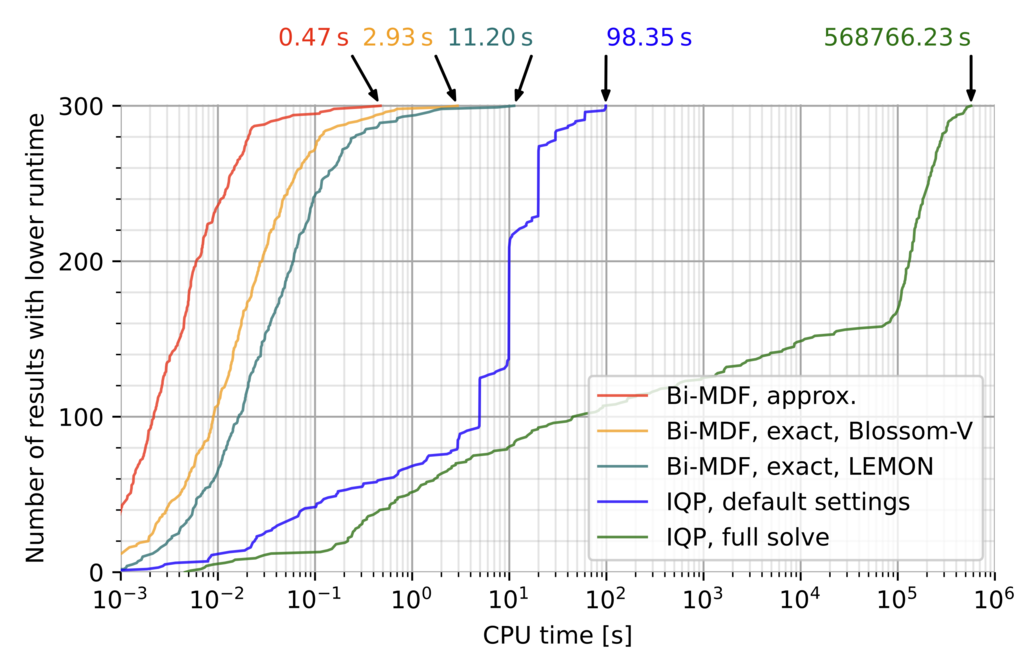
Fig. 15. Quad layouts via angle thresholded quantization on Knot100K (𝛼 = 45°) and Bunny (𝛼 = 20°). Models courtesy Aim@Shape & Stanford Computer Graphics Laboratory.

Fig. 16(a). Cumulative plot of achieved runtimes polygonal T-mesh quantization problems without alignment constraints on the 300 dataset. The full IQP solve reached its memory limit of 64GiB in 131 out of 301 cases.

BibTeX

@article{Heistermann:2023:BiMDF,
  author = {Heistermann, Martin and Warnett, Jethro and Bommes, David},
  title = {Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization},
  journal = {ACM Transactions on Graphics},
  volume = {42},
  number = {4},
  year = {2023},
  publisher = {ACM},
  address = {New York, NY, USA},
  doi = {10.1145/3592437}
}