Expansion Cones: A Progressive Volumetric Mapping Framework
Materials
SIGGRAPH Fast Forward video (20s)
SIGGRAPH Extended Talk (14min)
Abstract
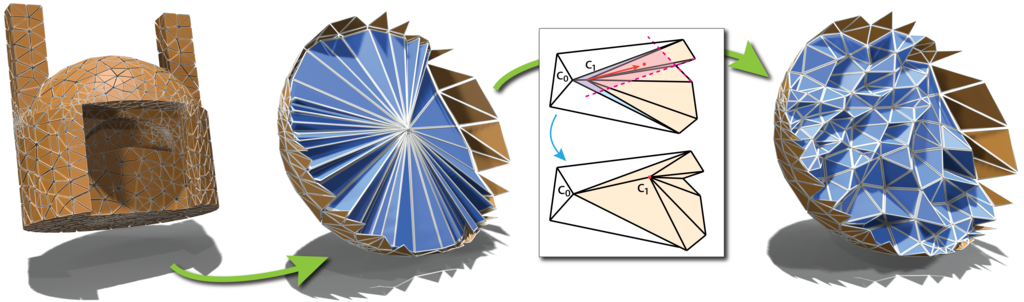
Volumetric mapping is a ubiquitous and difficult problem in Geometry Processing and has been the subject of research in numerous and various directions. While several methods show encouraging results, the field still lacks a general approach with guarantees regarding map bijectivity. Through this work, we aim at opening the door to a new family of methods by providing a novel framework based on the concept of progressive expansion. Starting from an initial map of a tetrahedral mesh whose image may contain degeneracies but no inversions, we incrementally adjust vertex images to expand degenerate elements. By restricting movement to so-called expansion cones, it is done in such a way that the number of degenerate elements decreases in a strictly monotonic manner, without ever introducing any inversion. Adaptive local refinement of the mesh is performed to facilitate this process. We describe a prototype algorithm in the realm of this framework for the computation of maps from ball-topology tetrahedral meshes to convex or star-shaped domains. This algorithm is evaluated and compared to state-of-the-art methods, demonstrating its benefits in terms of bijectivity. We also discuss the associated cost in terms of sometimes significant mesh refinement to obtain the necessary degrees of freedom required for establishing a valid mapping. Our conclusions include that while this algorithm is only of limited immediate practical utility due to efficiency concerns, the general framework has the potential to inspire a range of novel methods improving on the efficiency aspect.
BibTeX
@article{Nigolian:2023:SchrEx,
author = {Nigolian, Valentin Z. and Campen, Marcel and Bommes, David},
title = {Expansion Cones: A Progressive Volumetric Mapping Framework},
journal = {ACM Transactions on Graphics},
volume = {42},
number = {4},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
doi = {10.1145/3592421}
}