AlgoHex Publications
-
HexHex: Highspeed Extraction of Hexahedral Meshes
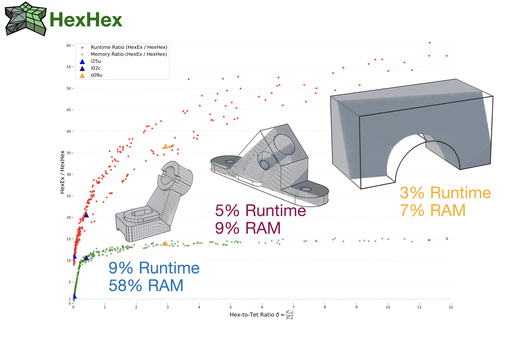
Modern hexahedral mesh generation relies on integer-grid maps (IGM), which map the Cartesian grid of integer iso-surfaces to a structure-aligned and conforming hexahedral cell complex discretizing the target shape. The hexahedral mesh is formed by iso-surfaces of the map such that an extraction algorithm is needed to convert the implicit map representation into an explicit mesh. State-of-the-art algorithms have been designed with two goals in mind, i.e., (i) unconditional robustness and (ii) tolerance to map defects in the form of inverted or degenerate tetrahedra. Because of significant advancements in the generation of locally injective maps, the tolerance to map defects has become irrelevant. At the same time, there is a growing demand for efficiently handling significantly larger mesh complexities, unfortunately not well served by the state-of-the-art since the tolerance to map defects induces a high runtime cost. Consequently, we present HexHex, a novel (unconditionally robust) hexahedral mesh extraction algorithm for locally injective integer-grid maps designed for maximal performance and scalability. Key contributions include a novel and highly compact mesh data structure based on so-called propellers and a conservative rasterization technique, significantly reducing the number of required exact predicate tests. HexHex not only offers lower asymptotic runtime complexities from a theoretical perspective but also lower constants, enabling in practice a 30x speedup for medium-sized examples and a larger speedup for more complex inputs, specifically when the hex-to-tet ratio is large. We provide a C++ reference implementation, supporting multi-core parallelization and the extraction of curved (piecewise-linear) hexahedral mesh edges and faces, e.g., valuable for subsequent higher-order mesh generation.
@article{Kohler:2025:hexhex, author = {Kohler, Tobias and Heistermann, Martin and Bommes, David}, title = {{HexHex: Highspeed Extraction of Hexahedral Meshes}}, journal = {ACM Transactions on Graphics}, volume = {44}, number = {4}, year = {2025}, publisher = {ACM}, address = {New York, NY, USA}, doi = {10.1145/3730940} } -
Feature-Aligned Parametrization in Penner Coordinates
Parametrization is a key element of many geometric modeling tasks. Seamless parametrization, in particular, is needed as a starting point for many algorithms for quadrangulation and conversion to high-order patches, as well as for the construction of seamless texture maps and displacement maps. Seamless parametrizations are difficult to compute robustly, in part because, in general, it is not known if one exists for a given mesh connectivity or for a particular configuration of singularities. Recently, Penner-coordinate-based methods that allow for connectivity changes have been shown to achieve a perfect success rate on a widely used dataset (Thingi10k). However, previously proposed Penner coordinate methods do not support sharp feature alignment or soft alignment with preferred directions on the surface, both of which are important for practical applications, especially those involving models with sharp features. In this paper, we extend Penner coordinates to surfaces with sharp features to which the parametrization needs to be aligned. Our algorithm extends the holonomy signature description of seamless parametrizations to surfaces with marked feature curves. We describe sufficient conditions for obtaining feasible solutions and describe a two-phase method to efficiently enforce feature constraints or minimize residual errors when solutions are unattainable. We demonstrate that the resulting algorithm works robustly on the Thingi10k dataset with automatic feature labeling, and the resulting seamless parametrizations can be optimized, quantized, and quadrangulated, completing the quad mesh generation pipeline.
@article{Capouellez:2025:feature-aligned-penner-param, author = {Capouellez, Ryan and Singh, Rodrigo and Heistermann, Martin and Bommes, David and Zorin, Denis} title = {{Feature-Aligned Parametrization in Penner Coordinates}}, journal = {ACM Transactions on Graphics}, volume = {44}, number = {4}, year = {2025}, publisher = {ACM}, address = {New York, NY, USA}, doi = {10.1145/3731216} } -
Quad Mesh Quantization Without a T-Mesh
Grid preserving maps of triangulated surfaces were introduced for quad meshing because the 2D unit grid in such maps corresponds to a sub-division of the surface into quad-shaped charts. These maps can be obtained by solving a mixed integer optimization problem: Real variables define the geometry of the charts and integer variables define the combinatorial structure of the decomposition. To make this optimization problem tractable, a common strategy is to ignore integer constraints at first, then to enforce them in a so-called quantization step. Actual quantization algorithms exploit the geometric interpretation of integer variables to solve an equivalent problem: They consider that the final quad mesh is a sub-division of a T-mesh embedded in the surface, and optimize the number of sub-divisions for each edge of this T-mesh. We propose to operate on a decimated version of the original surface instead of the T-mesh. It is easier to implement and to adapt to constraints such as free boundaries, complex feature curves network etc.
@article{quantization-without-tmesh, author = {Coudert-Osmont, Yoann and Desobry, David and Heistermann, Martin and Bommes, David and Ray, Nicolas and Sokolov, Dmitry}, title = {Quad Mesh Quantization Without a T-Mesh}, journal = {Computer Graphics Forum}, doi = {https://doi.org/10.1111/cgf.14928}, } -
Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization
Subdividing non-conforming T-mesh layouts into conforming quadrangular meshes is a core component of state-of-the-art (re-)meshing methods. Typically, the required constrained assignment of integer lengths to T-Mesh edges is left to generic branch-and-cut solvers, greedy heuristics, or a combination of the two. This either does not scale well with input complexity or delivers suboptimal result quality. We introduce the Minimum-Deviation-Flow Problem in bi-directed networks (Bi-MDF) and demonstrate its use in modeling and efficiently solving a variety of T-Mesh quantization problems. We develop a fast approximate solver as well as an iterative refinement algorithm based on graph matching that solves Bi-MDF exactly. Compared to the state-of-the-art QuadWild implementation on the authors' 300 dataset, our exact solver finishes after only 0.49% (total 17.06s) of their runtime (3491s) and achieves 11% lower energy while an approximation is computed after 0.09% (3.19s) of their runtime at the cost of 24% increased energy. A novel half-arc-based T-Mesh quantization formulation extends the feasible solution space to include previously unattainable quad meshes. The Bi-MDF problem is more general than our application in layout quantization, potentially enabling similar speedups for other optimization problems that fit into the scheme, such as quad mesh refinement.
@article{Heistermann:2023:BiMDF, author = {Heistermann, Martin and Warnett, Jethro and Bommes, David}, title = {Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization}, journal = {ACM Transactions on Graphics}, volume = {42}, number = {4}, year = {2023}, publisher = {ACM}, address = {New York, NY, USA}, doi = {10.1145/3592437} }